LeetCode 98. Validate Binary Search Tree

鐵人賽程式設計 12th鐵人賽 13th鐵人賽 2019鐵人賽

John Lu

團隊捲土重來的Kotlin鐵人們

2023-09-22 00:06:04

350 瀏覽

分享至

遞迴

解題思路

這道題目要求我們判斷一棵二元樹是否是二元搜尋樹。二元搜尋樹的特性是，對於任意一個節點，它的左子樹上所有節點的值都小於它，而它的右子樹上所有節點的值都大於它。

例如，下圖中的樹就是一個二元搜尋樹。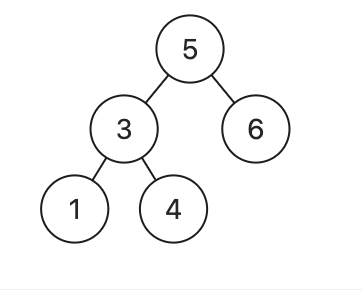

我們可以用一個遞迴函數 traverseRecursive(root, lower, upper) 來檢查以 root 為樹根的子樹是否在 (lower, upper) 的範圍內。如果 root 的值不在這個範圍內，則回傳 false；否則，繼續檢查它的左右子樹是否符合條件。初始時，我們設置 lower 和 upper 為無窮小和無窮大。

以下是遞迴函數的 iterations：

root	lower	upper	result
5	-inf	+inf	true
3	-inf	5	true
1	-inf	3	true
null	-inf	1	true
4	3	5	true
null	3	4	true
null	4	5	true
6	5	+inf	true
null	5	6	true
null	6	+inf	true

Recap

你能說明為什麽在遞迴呼叫左子樹時，我們要把上界設為 root 的值嗎？

迎接面試挑戰，不再孤軍奮戰！
一起來寫一份無懈可擊的履歷表，好好展現你傲人的經歷！在投遞履歷前，不妨先安排履歷諮詢，確保你的履歷脈絡清晰。搭配簡潔且專業的履歷模板工具，可以讓你在履歷表上呈現最好的自己。
現在就加入 Line 讀書會，邁向成功的第一步！

　履歷諮詢 　加入讀書會 (邀請碼：3087)

程式

class Solution {
    fun isValidBST(root: TreeNode?): Boolean {
        return traverseRecursive(root)
    }

    private fun traverseRecursive(root: TreeNode?, lower: Long, upper: Long): Boolean {
        return root?.let {
            val value = root.`val`.toLong()
            value in (lower + 1) until upper
                    && traverseRecursive(it.left, lower, value)
                    && traverseRecursive(it.right, value, upper)
        } ?: true
    }
}

複雜度分析

時間複雜度:
$on$ ，其中 $n$ 是二元樹中的節點個數。在遞迴呼叫時，二元樹的每個節點最多被訪問一次，因此時間覆雜度為 $on$ 。
空間複雜度:
$on$ ，其中 $n$ 是二元樹中的節點個數。遞迴函數在遞迴的過程中，需要為每一層遞迴函數分配堆疊空間，所以空間複雜度取決於遞迴的深度，即二元樹的高度。最壞情況下二元樹為歪斜二元樹，樹的高度為 $n$ ，遞迴最深達到 $n$ 層，所以最壞情況下空間複雜度為 $on$ 。